از ماجرای لباس آبی/طلایی تا مباحثات بور–اینشتین

طی روزهای گذشته گویی کاربران اینترنت به دو دسته تقسیم شده‌اند: آن‌هایی که لباس زیر را به رنگ آبی-مشکی می‌بینند و آن‌هایی که همین لباس را به رنگ سفید-طلایی می‌بینند. وب‌سایت‌ها و صاحب‌نظران متعددی تاکنون در این‌باره به اظهار نظر پرداخته و سعی در توجیه این موقعیت متناقض کرده‌اند.

در این مقاله ‌می‌کوشم از زاویه‌ای دیگر به ماجرا بنگرم: اینکه این موضوع ظاهراً بامزه را می‌توان مقدمه‌ای برای درک یکی از تکان‌دهنده‌ترین مقاطع تاریخ علم فیزیک برشمرد: امسال هشتادمین سالگرد انتشار مقاله‌ای جنجالی است که نقطه عطفی را در مباحثات بی‌سرانجام دو غول دنیای فیزیک رقم زد: آلبرت اینشتین و نیلز بور (Niels Bohr) – دو فیزیکدان دوران‌سازی که «واقعیت» را به دو صورت می‌دیدند.

ماجرا برمی‌گردد به اوایل ماه فوریه امسال؛ وقتی‌که سیسیلیا بلیسدل لباسی را از فروشگاه انگلیسی Roman Originals سفارش داد تا برای شرکت در عروسی قریب‌الوقوع دخترش، گریس، آن را به تن کند. او عکسی از این لباس تهیه کرد و برای گریس و دختر دیگرش آنگی فرستاد. اما «چرا می‌خواد توی عروسی، سفید و طلایی بپوشه؟» این را گریس در ایمیلی به آنگی نوشت. آنگی به بیزینس‌اینسایدر می‌گوید: «از اینکه مادرم یک لباس روشن انتخاب کرده بود، شوکه شده بودیم».

جانستون، نامزد گریس هم رنگ لباس را نپسندید و عکس مزبور را روی حساب فیس‌بوک‌ خود منتشر کرد. همان‌جا بود که بحث بالا گرفت. این‌بار دوست نوازنده جانستون، کیتلین مک‌نیل هم – که بعداً در عروسیشان اجرای موسیقی داشت – عکس را روی حساب تامبلر مدیر برنامه‌هایش، سارا ویچل، به اشتراک گذاشت و نوشت: «بچه‌ها لطفاً کمک – این لباس سفید و طلایی‌ایه یا آبی و مشکی؟ من و دوستام نمی‌تونیم به تفاهم برسیم و اعصاب‌مون خرده».

اولین بیننده، در کامنتی نوشت: «بچه‌های کلاسم بحث‌شون گرفته بود. نصف‌شون مشکی و آبی می‌بینن، نصف دیگه‌شون طلایی و سفید. یکی لطفاً توضیح بده». و مک‌نیل در جوابش نوشت: «اگر این طلایی نباشه، کل زندگی‌م یه چاخان بوده».

«واقعیت» چیست؟ آیا می‌توان این اختلاف نظر را به اختلاف ساختار «چشم» یا حتی «مغز» بینندگان این عکس نسبت داد؟ یا ما با یک خطای دید ساده مواجه‌ایم؟

از آنجاکه می‌دانیم این لباس واقعاً به رنگ آبی و مشکی است، حصول یک توضیح علمی در این‌باره چه بسا امکان‌پذیر باشد: اگرچه الگوی رنگ‌بندی این لباس «واقعاً» ثابت است، اما می‌توان تعابیر مختلفی از الگوی نور‌پردازی محیطی که در آن این لباس عکاسی شده، صورت داد.

جهت تصور این الگو نیاز است که ابتدا «معیار» را برای واقعیت رنگ‌ها تعریف کرد؛ و این معیار، نور سفید است. ما از آنجایی می‌دانیم این لباس واقعاً به رنگ آبی و مشکی است، که در عکس رسمی و تبلیغاتی شرکت تولیدکننده، ما لباس را در نور کاملاً سفید می‌بینیم.

تنظیمات وایت‌بالانس و معضل «معیار»

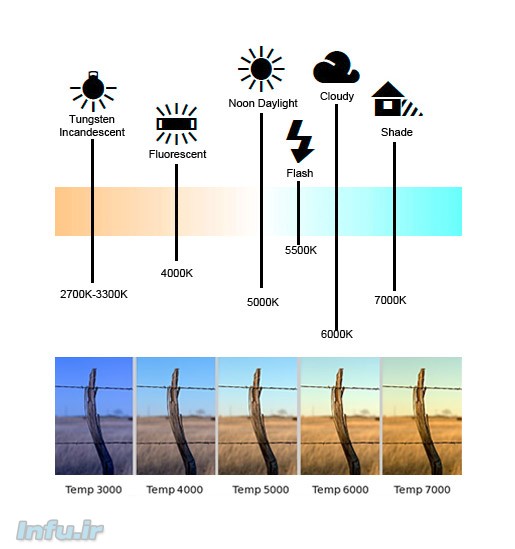
چنانچه با دوربین‌های عکاسی دیجیتال نیمه‌حرفه‌ای (یا حرفه‌ای) آشنا بوده باشد، با تنظیمات «وایت‌بالانس» (White Balance) دوربین نیز آشنایی دارید. در حدفاصل فشردن دکمه شا‌تر و ثبت عکس تا نمایش آن در نمایشگر دوربین، داده‌های دریافتی از طریق حسگر، طی چند مرحله – از جمله تنظیمات وایت‌بالانس – پردازش اولیه می‌شوند.

در این مرحله، دوربین ابتدا محدوده روشنی از عکس را انتخاب می‌کند و بر مبنای میزان «سفید» بودن آن محدوده، به نورسنجی (یا به عبارت دقیق‌تر، «کلوین‌سنجی») باقی نقاط عکس می‌پردازد تا بدین‌وسیله ما بتوانیم الگوی واقعی رنگ‌های منظره را در عکس نهایی مشاهده کنیم. اما آن محدوده روشن – که می‌توان آن را «محدوده معیار» نامید – در تمام شرایط نوری کاملاً سفید نیست. یک برگ کاغذ سفید، چنانچه در زیر سایه قرار داده شود، آبی کدر (یا خاکستری) به نظر می‌رسد، و چنانچه در زیر لامپ هالوژن، اندکی زرد.

اما دوربین متوجه نیست که یک کاغذ در تمام این شرایط «واقعاً» به رنگ سفید است؛ لذا در بخش تنظیمات وایت‌بالانس دوربین، چند وضعیت پیش‌فرض را می‌بینیم که عکاس با انتخاب‌ هرکدامشان برای دوربین معلوم می‌کند که شرایط نوری محیط عکاسی وی هم‌اینک چگونه است:

دوربین، رنگ سفید را تنها در «نور آفتاب ظهرگاهی» به‌صورت رنگ سفیدی که ما می‌شناسیم، می‌شناسد؛ و بر همین مبنا سایه را رنگ «سفید» ی تعریف می‌کند که نور آبی بر آن بتابد، و «رنگ غروب» را هم رنگ «سفید» ی که نور زرد بر آن تابیده باشد. به همین منوال، دوربین به نوعی «دماسنجی» (یا‌‌ همان کلوین‌سنجی) رنگ‌ها متوسل می‌شود، به‌طوریکه نقطه صفر این کلوین‌سنج فرضی، مفهوم «سفید» است و سایر مفاهیم رنگی بر مبنای «سرد‌تر» یا «گرم‌تر» بودنشان نسبت به رنگ سفید طبقه‌بندی و مشخص می‌شوند. اما ما در اشارات روزمره‌مان به مفاهیم رنگی، برای هر رنگ، معیاری منحصربه‌فرد قائلیم – که‌‌ همان «نام» این رنگ‌هاست.

رنگ سفید در واقع آمیزه‌ای از تمام رنگ‌های طیف نور مرئی است و فی‌نفسه طول موج مشخصی را نمی‌توان به آن نسبت داد. با این‌همه، چنانچه دقت کنیم، باقی نام‌هایی که در زبان روزمره‌مان به مفاهیم رنگی اطلاق می‌کنیم نیز همین‌گونه‌اند: «قرمز» طول موج‌های متعددی را تحت پوشش خود دارد، و همین‌طور «آبی»، «زرد»، و…. لذا این مفاهیم کیفی (که از این پس آن‌ها را «مفاهیم کلاسیک» خواهیم خواند)، در علم فیزیک معنای دقیق و واضحی ندارند؛ چراکه معیار کلوین‌سنجی نور در چارچوب فیزیک، نه یک معیار کیفی (نظیر مفهوم «سفید»)، بلکه معیاری کمی (یعنی طول موج) است.

برخلاف مفاهیم کمی و واضح علم فیزیک، مفاهیم کلاسیک را نمی‌توان به‌صورت یک طیف به‌هم‌پیوسته مجسم کرد، چراکه به رغم تبدیل «تدریجی» رنگ زرد به نارنجی، ما هیچ مفهومی به غیر از این دو مفهوم کلاسیک (یا آمیزه‌ای از سایر مفاهیم کلاسیک، نظیر «زرد آکریلیک» و…) را به‌منظور توصیف وضعیت‌های میانگین استفاده نمی‌کنیم.

جی نیتز، از عصب‌شناسان دانشگاه واشنگتن، عکسی که سیسیلیا بلیسدل از لباس خود گرفته را مصداق یک وضعیت میانگین می‌داند: «من ۳۰ سال است که مشغول بررسی اختلافات افراد در بینایی رنگی هستم، و این‌ یکی از برجسته‌ترین اختلافات بین‌فردی‌ای است که تابه‌حال دیده‌ام» – این‌که عده‌ای لباس را آبی-مشکی می‌بینند و عده‌ای سفید-طلایی. ما می‌دانیم که به‌هنگام ثبت این عکس، طیف معینی از طول موج‌ها به لنز دوربین وارد شده‌ بوده‌اند و همچنین طیف معینی از طول‌ موج‌ها نیز از صفحه نمایشگر رایانه به چشممان می‌رسند. اما چرا با این‌وجود، افراد در تعیین رنگ لباس اختلاف نظر دارند؟

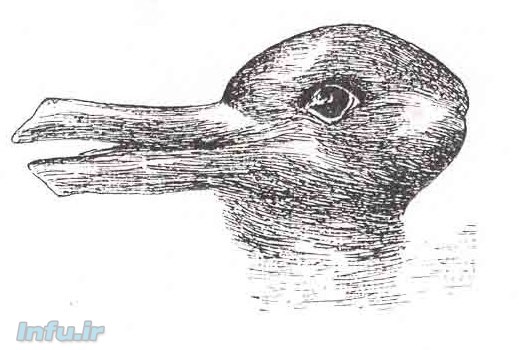
مسأله اختلاف در تفسیر وضعیت‌های میانگین را نخستین بار فلاسفه بودند که به هیأت یک «مسأله» مطرح کردند. لودویگ ویتگنشتاین، فیلسوف برجسته اتریشی، در فقره ۱۱۸ از بخش دوم «پژوهش‌های فلسفی» (ویراست ۲۰۰۹)، این مسأله را با اشاره به تصویر معروف اردک-خرگوش مطرح می‌کند.

ما نمی‌توانیم این تصویر را به‌صورت یک اردک و «همزمان» به‌صورت یک خرگوش (یا بالعکس) تماشا کنیم؛ بلکه در هر مرتبه، تنها یکی از این دو را تشخیص می‌دهیم. سؤال اینجاست که بین «اردک‌بودگی» و «خرگوش‌بودگی» این تصویر دوپهلو چه نسبتی برقرار است؟ ما معمولاً از این نسبت با عنوان ساده «خطای دید» یاد می‌کنیم، اما در خصوص عکس لباس بلیسدل مایل‌ایم ببینیم که «واقعیت» چیست (ولو هم‌اینکه دچار خطا شده باشیم)؟

برای پاسخ به این سؤال، بایستی رجوعی به بحث سابقمان در رابطه با تنظیمات وایت‌بالانس دوربین داشت: معیار عکاسانه «واقعیت رنگی»، مفهوم کلاسیک «سفید» است. لذا می‌توان پرسید: «معیار کلاسیک» واقعیت رنگی (مثلاً معیار واقعیت داشتن رنگ «سفید» نزد خودمان) چه می‌تواند باشد؟

پاسخ، تمایز تقلیل‌ناپذیر مفاهیمی است که ما در زبان روزمره‌مان حین اشاره به رنگ‌ها به کار می‌بندیم. این‌که نمی‌توان از مفاهیم کلاسیک در توصیف پیوستار طیف رنگ‌ها استفاده کرد از بابت تقلیل‌ناپذیری متقابل مفاهیمی است که ما در زبانمان حین اشاره به رنگ‌ها به کار می‌بندیم (همچون تقلیل‌ناپذیری مفهوم «اردک» به «خرگوش»، و بالعکس). این موضوع اما به مفاهیم «رنگی» محدود نمی‌شود، بلکه اساساً دو مفهوم کلاسیکی‌ که در توصیف واقعیت استفاده می‌شود را نمی‌توان به یکدیگر تقلیل داد؛ مثلاً «سایه» و «نور» (ما در جهان واقع، یا «سایه» را می‌بینیم، یا «نور» را؛ نه هر دو را همزمان).

عکس لباس بلیسدل از این‌رو گمراه‌کننده است که در آن معیار کلاسیک واقعیت رنگ «سفید» با معیار عکاسانه واقعیت رنگی (یعنی‌‌ همان مفهوم «سفید») همپوشانی دارد.

ساده می‌توان تصور کرد که چنانچه این عکس، یک نقاشی می‌بود (نظیر اردک-خرگوش)، چنین بحث درازدامنی را در فضای مجازی به راه نمی‌انداخت و تمام بینندگانش آن را به حساب یک «خطای دید» ساده می‌گذاشتند. اما ما «عکس» لباس بلیسدل را می‌بینیم و بر مبنای «واقعیت» داشتن‌ آن اقدام به تعیین رنگ‌های آن می‌کنیم. اما در قضاوت‌مان حول «معیار» واقعیت رنگی دچار گمراهی می‌شویم: در موقعیت‌های روزمره، ما رنگ سفید را بر مبنای تمایز تقلیل‌ناپذیر دو مفهوم «نور» و «سایه» تشخیص می‌دهیم (به‌طوری‌که چنانچه بدانیم جسمی در «سایه» است و در عین‌حال دم به کبودی می‌زند، نتیجه می‌گیریم که این جسم «در واقع» سفیدرنگ است).

اما در عکس لباس بلیسدل، ما در تشخیص این‌که آیا لباس در «نور» واقع شده یا «سایه» دچار تردیدیم، چراکه برای تعیین رنگ لباس، پیرو معیار عکاسانه واقعیت رنگی، محتاج کلوین‌سنجی از محدوده‌های روشن روی لباس هستیم، و در عین‌حال این را هم نمی‌دانیم که آن محدوده‌های معیار آیا خود در نور واقع شده‌اند یا سایه. لذا قابل فهم است که عده‌ای الگوی رنگی این لباس را آبی-مشکی تفسیر کنند و عده‌ای سفید-طلایی (تصویر پایین، کادر چپ).

اما آیا می‌توان به این سؤال هم پاسخ داد که «چرا» عده‌ای آن را آبی-مشکی تفسیر می‌کنند و عده‌ای دیگر سفید-طلایی؟ (همان‌طور که می‌توان پرسید چرا عده‌ای طرح «اردک-خرگوش» را به‌صورت اردک می‌بینند، و عده‌ای دیگر – یا حتی خودمان در موقعیتی دیگر – آن را به‌صورت خرگوش؟). در واقع شگفتی بینندگان این عکس، از کنجکاویشان بابت دانستن پاسخی احتمالی به همین پرسش‌ ناشی می‌شود. اما نخست باید دید آیا یافتن یک پاسخ منطقی به این پرسش اساساً «امکان‌پذیر» هست یا نه؟

برای تصور این‌که تمام بینندگان عکس لباس بلیستل شاهد موضوعی «واحد» هستند (که آن را به «دو» طریق می‌بینند)، باید معیاری برای واقعیت داشتن این موضوع واحد و بین‌الاذهانی یافت. (در واقع پاسخگویی به اینکه «چرا» بینندگان این لباس، آن را با دو رنگ‌بندی‌ متفاوت می‌بینند، منوط به معرفی معیاری برای واقعیت داشتن این موضوع بین‌الاذهانی است). سابقاً گفتیم که ما رنگ‌بندی عکس لباس بلیسدل را به دو طریق می‌بینیم چون تفسیرمان از نواحی روشن لباس در شرایطی صورت می‌پذیرد که معیار کلاسیکی واقعیت رنگ «سفید» نزد ما با معیار عکاسانه واقعیت رنگی همپوشانی دارد؛ حال‌آنکه برای استنباط یک موضوع بین‌الاذهانی (که نقش واسط این دو تفسیر را ایفا می‌کند)، باید تفاوت‌ این دو تفسیر را از با ملاک قرار دادن معیار «عکاسانه» واقعیت رنگی استنباط کرد (چراکه ما به اعتبار «عکس» بودن این تصویر است که امکان وجود یک موضوع بین‌الاذهانی را محتمل می‌انگاریم، حال‌آنکه کنجکاو واقعیت داشتن یا نداشتن مابه‌ازای خارجی یک نقاشی، مثلاً طرح «اردک-خرگوش» نیستیم). اما در این صورت به یک تناقض آشکار برخواهیم خورد (تصویر پایین، کادر راست).

سابقاً اشاره شد که دوربین عکاسی واقعیت داشتن رنگ‌ها را بر حسب معیار «سفید» می‌سنجد. در تنظیمات وایت‌بالانس دوربین، مفاهیم «نور» و «سایه» به خودی خود فاقد معنایی مشخص‌اند و رنگ‌ها بر حسب «دمای نور» (و طبق فرآیندی موسوم به کلوین‌سنجی) بازتعریف می‌شود. لذا چنانچه دلیل دوپهلو بودن عکس لباس بلیستل را مطابق معیار «عکاسانه» واقعیت رنگی بسنجیم، می‌‌بایستی نخست – از طریق برهان خُلف – به بازتعریف مفاهیم «نور» و «سایه» بر حسب رنگ‌بندی این عکس بپردازیم.

اما از این تحلیلمان چنین نتیجه خواهد شد که طبق معیار عکاسانه واقعیت رنگی، ما «واقعاً» دو لباس متفاوت داریم (یکی لباس سفید-طلایی، و یکی لباس آبی-مشکی)؛ چراکه از دید دوربین عکاسی، محدوده سایه دارای «رنگ سرد»، و محدود روشن، به طریق نسبی، دارای «رنگ گرم» تعریف می‌شود – حال‌آنکه می‌دانیم رنگ «ذاتی» یک جسم، با قرار دادن آن در نور یا سایه تغییر نخواهد کرد. از طرفی می‌دانیم که در واقع «یک» لباس هم بیشتر نداشته‌ایم. از این تناقض اینطور نتیجه می‌شود که:

نمی‌توان بر مبنای اختلاف نظر بینندگان عکس لباس بلیستل بر سر رنگ‌بندی این لباس، معیاری را برای «واقعیت داشتن» یک موضوع واسط و بین‌الاذهانی (جهت مقایسه اختلافات مشاهداتی بینندگان این عکس) استنتاج کرد. لذا پاسخ به این سؤال که: «چرا بینندگان این لباس، آن را با دو رنگ‌بندی متفاوت می‌بینند؟»، منطقاً امکان‌پذیر نیست.

اما آیا این بدین‌معناست که هیچ پاسخی به سؤال فوق «وجود» ندارد؟ یا اینکه وجود دارد و امکان ندارد که «ما» به آن پی ببریم؟

دیدیم که استنباط معیاری برای امکان‌پذیری طرح یک پاسخ خرسندکننده به این سؤال از رهگذر رابطه علیت، به تناقض خواهد انجامید. اما چنانچه ضرورتی در استنتاج علّی «یک موضوع واسط و بین‌الاذهانی» احساس نکنیم، این سؤال خودبه‌خود منحل خواهد (همان‌طور که هیچ‌کس درصدد استنتاج «وجود داشتن» موجودی به نام اردک-خرگوش نیست). در این صورت می‌توان گفت که ما به روایت «تقلیل‌پذیر» از رابطه علیت پشت پا زده‌ایم. این قطعاً حکم جسورانه‌ای خواهد بود؛ اما چنان‌چه آن را در پرتو تحول نگاه فیزیک معاصر از مفهوم «واقعیت فیزیکی» بررسی کنیم، این تصمیم‌مان چندان بعید به نظر نخواهد رسید.

امسال هشتادمین سالگرد صورت‌بندی معمایی راجع به معیار «واقعیت فیزیکی» است که اساس تصورمان از مفهوم «واقعیت» را دگرگون ساخت؛ دستاوردی آنچنان اعجاب‌انگیز که شگفتی‌مان از بابت دوپهلو بودن رنگ‌های لباس بلیستل را کم‌فروغ خواهد کرد – معمای EPR.

معمای EPR و معضل «محاسبه»

در سال ۱۹۲۷، فیزیکدان آلمانی ورنر هایزنبرگ موفق شد روابطی را از مبانی ریاضی نظریه کوانتوم استنتاج کند که مطابق آن‌ها تعیین مکان و سرعت «دقیق» یک ذره زیراتمی، به نحو همزمان ممکن نیست. هایزنبرگ خود کوشید این روابط – موسوم به «روابط عدم قطعیت» – را با طرح یک آزمایش ذهنی ساده، اینچنین ملموس جلوه دهد: تعیین مکان یک ذره، طبیعتاً مستلزم «تشخیص» آن ذره است، و این خود مستلزم برهم‌کنش ذره با پرتوهای نوری که به چشم ناظر می‌رسند.

چنانچه یک میکروسکوپ فوق‌دقیق می‌داشتیم که می‌توانست مکان یک ذرهٔ زیراتمی (فرضاً یک الکترون) را – با تاباندن پرتوهای نور بر آن – تعیین کند، در همین اثناء سرعت ذره – به‌واسطه انتقال تکانهٔ پرتوهای گسیلی به ذره – دستخوش تغییر می‌شد. این در حالی است که بدون تاباندن پرتو‌ها هم تعیین مکان دقیق ذره برای ناظر امکان‌پذیر نیست. لذا تعیین مکان و سرعت ذاتی یک ذره، به نحو همزمان غیرممکن است. در این تعبیر، واقعیت داشتن فیزیکی ذره مفروض گرفته شده است و عدم قطعیت به مثابه محدودیتی در برابر «ناظر» معرفی می‌شود.

با این‌همه، تعبیر هایزنبرگ از مفهوم عدم قطعیت کوانتومی – که دلالت بر محدودیت قوای تشخیصی فرد ناظر دارد – منطقاً نارساست. در چارچوب نظریه سنّتی کوانتوم، «مکان» یک ذره عملاً از معیارهای «واقعیت» آن ذره محسوب می‌شود، و آنچه در ابتدا مفروض گرفته می‌شود چیزی به جز «بی‌نقص بودن» نظریه کوانتوم نیست؛ حال‌آنکه در چارچوب تعبیر هایزنبرگ، برعکس، از‌‌ همان ابتدا واقعیت فیزیکی ذره مفروض گرفته می‌شود، آن‌هم به این اعتبار که ذره واجد ویژگی‌هایی فیزیکی، از جمله «مکان» است – ولو مکان آن هنوز تعیین نشده باشد. لذا چارچوب منطقی تعبیر هایزنبرگ، ریشه در یک برهان خُلف دارد.

بدین‌وسیله تلاش برای یافتن تعبیری موثّق‌تر از روابط عدم قطعیت، رفته‌رفته زمینه‌ساز یکی از ژرف‌ترین مجادلات فلسفی تاریخ علم شد: مباحثات بور-اینشتین.

نیلز بور، از بنیانگذاران نظریه کوانتوم، در‌‌ همان سال ۱۹۲۷، ضمن تأکید بر فرض بی‌نقص بودن نظریه کوانتوم، روابط عدم قطعیت را شاهدی بر این مدّعا گرفت که روایت تقلیل‌پذیر از رابطه علّیت در توصیف «واقعیت فیزیکی» ناکام خواهد ماند. جایگزین پیشنهادی بور، تلقی‌ دیگری از رابطه علیت بود که وی آن را رابطه «مکملیّت» (complementarity) نامید.

مطابق تلقی بور، معیارهای معرّف پدیدارهای کوانتومی، آن‌گونه روابطی بین کمّیت‌های کلاسیک فیزیک هستند که «تعیین» آن پدیدار‌ها را – با امکان‌پذیری شرایط انجام محاسبه‌شان – امکان‌پذیر می‌کنند. از آنجاکه تعیین پدیدارهای مختلف کوانتومی (از جمله «سرعت» و «مکان» یک ذره)، شرایط محاسباتی مختلف و لذا روابط متفاوتی را هم بین کمّیت‌های کلاسیک ذى‌ربط می‌طلبد، معیار واقعیت هر پدیدار کوانتومی ضرورتاً منحصربفرد و غیرقابل تقلیل به معیار واقعیت یک پدیدار دیگر کوانتومی است (همان‌طور که معیارهای کلاسیک ناظر بر واقعیت داشتن هر رنگ، قابل تقلیل به یکدیگر نیستند). به‌همین‌واسطه هم تغییر ناگزیر شرایط محاسباتی با هدف شناخت هرچه‌بهتر یک ذره، لاجرم منجر به تعیین پدیدارهایی «مانع‌الجمع» خواهد شد؛ به‌طوری‌که تعیین همزمان این پدیدار‌ها ممکن نخواهد بود. (این نه بدین‌معناست که «واقعیتی»‌ مستقل از آنچه می‌توان محاسبه کرد، وجود ندارد، بلکه بدین‌معناست که استنباط «واقعیت داشتن» یک پدیدار کوانتومی از طریق معیار واقعیت یک پدیدار کوانتومی دیگر، نه از طریق روایتی «تقلیل‌پذیر» از رابطه علیت، و تمهید یک مفهوم واسطه – همچون: ذره به مثابه یک گوی بیلیارد – بلکه از طریق رابطه «مکملیت» امکان‌پذیر است).

اما استدلال فلسفی بور از دید قاطبه فیزیکدانان، به‌ویژه اینشتین، قانع‌کننده نبود. اینشتین ضمن تأکید بر «واقعیت داشتن» روایت تقلیل‌پذیر از علیّت، مدعی بود که روابط عدم قطعیت، شاهدی بر «نقصان» نظریه کوانتوم، و ناکامی این نظریه از ارائه یک‌ توصیف کامل از طبیعت است. او با صورت‌بندی سلسله‌آزمایشاتی ذهنی در حدفاصل سال‌های ۱۹۲۷ تا ۱۹۳۰ کوشید تعیین همزمان سرعت و مکان دقیق یک ذره زیراتمی را امکان‌پذیر جلوه دهد.

اما بور از طریق تبیین الگوی امکان‌پذیرى محاسبه در چارچوب این آزمایشات ذهنی، امتناع چنین امکانی را واضحاً نشان می‌داد. باری عاقبت هشتاد سال پیش، در سال ۱۹۳۵، اینشتین به اتفاق دو فیزیکدان دیگر به نام‌های بوریس پادولسکی و ناتان روزن، در مقاله‌ای تحت عنوان «آیا توصیف مکانیک کوانتومی از واقعیت فیزیکی را می‌توان کامل پنداشت؟» (که بعد‌ها مطابق حرف نخست نام نویسندگانش، به‌ مقاله EPR معروف شد)، آزمایشی ذهنی را طراحی کردند که امکان تعیین همزمان سرعت و مکان یک ذره، این‌بار «بدون هیچ‌گونه برهم‌کنشی با ابزارآلات محاسباتی» را می‌سر می‌ساخت. امتیاز این آزمایش در نسبت با آزمایشات ذهنی پیشین، ارائهٔ یک معیار کمّى براى مفهوم «واقعیت فیزیکی» بر مبنای روایتی تقلیل‌پذیر از علیت بود.

آزمایش EPR اساساً بر این تصویر کوانتومى مبتنى است که چنانچه دو سیستم کوانتومى (فرضاً دو ذره) در ابتدا با یکدیگر برهم‌کنشى داشته باشند و سپس از یکدیگر جدا بیفتند، مادام‌که با هیچ سیستم دیگرى برهم‌کنش نکنند، وضعیت‌ هردویشان را مى‌توان با یک معادله‌ واحد (موسوم به «تابع موج») توصیف کرد.

لذا مى‌توان مکان (یا سرعت) دقیق ذره A را محاسبه کرد و از طریق تابع موجشان اقدام به استنباط مکان (یا سرعت) دقیق ذره B نمود. این بدین‌معناست که مى‌توان مکان و سرعت دقیق ذره B (که توأماً حاکی از «واقعیت داشتن» این ذره‌ هستند) را بدون اعمال هرگونه برهم‌کنشى بر آن ذره به دست آورد؛ حال‌آنکه نظریه کوانتوم، محاسبهٔ همزمان این دو کمیت وابسته به ذره B را ناممکن می‌داند. از این استدلال چنین نتیجه می‌شود که توصیف کوانتومى از واقعیت فیزیکى کامل نیست. در واقع چنانچه سه فرض: ۱) کامل بودن نظریه کوانتوم، ۲) کامل بودن مدعاى EPR، و ۳) واقعیت داشتن روایت تقلیل‌پذیر از رابطه علیت را همزمان روا بپنداریم، ناگزیر از پذیرش نتیجه‌ای نامعقول خواهیم بود: اینکه در صورت انجام محاسبه بر ذره A، ذره B نیز، هرچقدر هم که در دوردست واقع شده باشد، «بلافاصله» از این محاسبه تأثیر مى‌پذیرد (و در اینجا قید «بلافاصله» یعنى حتی سریع‌تر از سرعت نور، که مطابق روابط نسبیت خاص، سریع‌ترین راه ممکن انتقال اطلاعات در طبیعت محسوب مى‌شود). از آنجا که اینشتین حاضر به پذیرش این نتیجه خارق‌العاده نبود (چراکه نظریه کوانتوم را کامل نمى‌پنداشت)، با طعنه به چنین نتیجه‌اى، آن را «کنش شبح‌وار از راه دور» («spooky action at a distance») نامید.

با اینکه در آزمایش ذهنى EPR هیچ محاسبه‌اى «مستقیماً» بر ذره B اعمال نمى‌شود، اما تعیین مکان و سرعت دقیق آن از طریق محاسبه مکان و سرعت دقیق ذره A هم فقط هنگامى امکان‌پذیر است که ذره B پس از بر‌هم‌کنش اولیه‌اش با ذره A و پیش از اعمال فرآیند محاسبه ما بر ذره A، با «هیچ» سیستم دیگرى برهم‌کنش نداشته باشد. این بدین‌معناست که ذره B، علی‌رغم دست‌نخورده ماندن، ضرورتاً تحت «شرایط محاسباتى» کاملاً مشابهى با ذره A واقع است، و همین تشابه براى بور کافى بود تا با تکیه بر استدلال فلسفى سابق‌اش، در فرازی از جوابیه‌ی خود بنویسد: «… از آنجاکه این شرایط، مؤلفه‌اى ذاتى از توصیف هر پدیدارى که بتوان اصطلاح «واقعیت فیزیکى» بر آن اطلاق کرد را شکل مى‌دهند، مى‌بینیم که استدلال نویسندگان فوق، تضمین‌گر این نتیجه‌گیرىشان نیست که توصیف کوانتومی [از واقعیت فیزیکی] اساساً ناکامل است».

مدعای جسورانه بور بدین‌معنا بود که نظریه کوانتوم نه فقط کامل است، بلکه آنچه اینشتین آن را «کنش شبح‌وار از راه دور» مى‌نامد را هم عملاً روا مى‌دارد (اگرچه نه به نحوی که ناقض نسبیت خاص باشد). بور اساساً مدعی بود که فرض بر «واقعیت داشتن روایت تقلیل‌پذیر از رابطه علیت»، فرضی خطاست، و بایستی در عوض رابطه مکملیت را روا پنداشت.

با این‌حال، استدلال نویسندگان EPR، بور را متقاعد کرده بود که ایده مکملّیت او در حالی کماکان قابلیت پاسخ به استدلال آن‌ها را دارد که هنوز در حد یک استدلال «فلسفى» باقی مانده است، حال‌آنکه حریفان وی هم‌اینک موفق شده‌اند معیارى «فیزیکى» را براى «واقعیت فیزیکی» – بر مبناى روایتی تقلیل‌پذیر از علیت – عرضه کند. همین قدم از جانب نویسندگان مقاله EPR، بور را در باقى عمر حرفه‌ای‌اش مصمّم به یافتن معیارى «فیزیکى» براى اثبات ایده مکملیت ساخت – که البته در این زمینه قدمی از پیش برنداشت. این بدین‌معنا بود که استدلال EPR، از حیث فیزیکى همچنان بر ایده مکملیت بور ترجیح داشت.

اما در سال ١٩۶۴، جان بل، فیزیکدان ایرلندى، تحلیل هوشمندانه‌اى از مدعاى EPR عرضه کرد که در آن معیار «واقعیت فیزیکی» نزد نویسندگان مقاله EPR را مى‌شد به محک آزمون سپرد و بدین‌وسیله دست‌کم مدعاى «ناقص بودن» نظریه کوانتوم را عملاً ابطال (یا اثبات) نمود. طبق مدعاى EPR، مى‌توان مکان و سرعت دقیق ذره B (که بهترتیب آن‌ها را PB، و QB مى‌نامیم) را از طریق محاسبه مکان و سرعت دقیق ذره A (که به بهترتیب آن‌ها PA و QA می‌نامیم) محاسبه کرد. حال تصور کنید یک «متغیر پنهان» (H) نیز مى‌داشتیم که در صورت موفقیت نظریه کوانتوم در ارائه توصیفى صحیح از آن، این نظریه «کامل» مى‌شد. لذا محاسبه متغیر H در خصوص ذره B (یا HB) را مى‌شد از طریق محاسبه متغیر H در خصوص ذره A (یا HA) محاسبه کرد.

طبق مدعای EPR، از آنجاکه جملگى این شش متغیر را «مى‌توان» محاسبه کرد، آن‌ها همگی «واقعیت» نیز دارند. حال تصور کنید که جواب هرکدام از این متغیر‌ها دو حالت بیشتر نداشت: آرى یا نه. نویسندگان EPR فرض گرفته‌اند که پاسخ‌های PA و PB همواره یکسان‌اند؛ و همین‌طور پاسخ‌های QA و QB، و نیز پاسخ‌های HA و HB. حال تصور کنید که محاسبه سایر جفت‌متغیر‌ها به پاسخ‌هایى غیریکسان منجر مى‌شد (یعنى پاسخ جفت‌متغیرهاى PA/H»، PA/QB، QA/PB، QA/HB، «HA/QB، و «HA/PB»). لذا داریم: ١) پاسخ PB همواره یکسان با پاسخ PA، اما غیریکسان با پاسخ‌های QA و HA خواهد بود. در نتیجه، از طرفی: ۲) پاسخ‌های QA و HA همواره یکسان با هم، و در عین حال غیریکسان با پاسخ PA خواهد بود، و از طرف دیگر: ٣) از آنجاکه پاسخ HQ همواره یکسان با پاسخ‌هاى PA و HA است، پس پاسخ‌های PA و HA نیز همواره با هم یکسان خواهند بود. می‌بینیم که در این صورت گزاره ٣ با گزاره ١ متناقض از آب درخواهد آمد. تنها نتیجه‌اى که مى‌توان از این تحلیل گرفت این است که برخلاف مدعای EPR، اینطور نیست که تمام شش جفت‌متغیر نامبرده، «واقعیت» داشته باشند.

تحلیل بل فقط از یک جنبه با تحلیل حاضر تفاوت داشت: او به نسخه‌اى از آزمایش EPR استناد کرد که در آن چنین نیست که هر شش جفت‌متغیر نامبرده، «همواره» غیریکسان باشند، بلکه تنها در سه‌چهارم موارد غیریکسان‌اند. به عبارت دیگر: ١) پاسخ PB اگرچه همواره با پاسخ PA یکسان است، اما تنها در سه‌چهارم موارد با پاسخ‌هاى QA و HA غیریکسان است. یعنى: ۲) پاسخ‌های PA و HA (یا PA و QA) تنها در یک‌چهارم موارد یکسان‌اند. یک تحلیل احتمالاتى از گزاره‌هاى ١ و ٢ معلوم مى‌کند که QA و HA بایستى دست‌کم در نیمى از مواردْ یکسان باشند. اگر همین سلسلهٔ استدلالى را با شروع از پاسخ QB هم تکرار کنیم، به این نتیجه خواهیم رسید که پاسخ‌های PA و HA دست‌کم در نیمى از موارد یکسان‌اند.

اما در این صورت نیز باز به تناقض برمى‌خوریم: از طرفى پاسخ‌های PA و HA تنها در یک‌چهارم موارد یکسان‌اند، و از طرفى در نیمى از موارد یکسان‌اند. از این تحلیل هم ضرورتاً اینطور برمى‌آید که نبایستى تمام این شش جفت‌متغیر، «واقعیت» داشته باشند. بدین‌ترتیب اگر بتوان واقعیت داشتن این شش متغیر را با انجام دادن یک آزمایش EPR ثابت کرد، می‌توان «کامل بودن» نظریه کوانتوم را به چالش کشید.

از سال ١٩٧٢ تاکنون چندین و چند نسخه از آزمایش پیشنهادی EPR به ثمر رسیده است. در معروف‌ترین این آزمایشات، تیمى از فیزیکدانان فرانسوى به سرپرستى آلن اسپه (Alain Aspect)، سه آزمایش را در حدفاصل سال‌هاى ١٩٨١ و ١٩٨٢ به ثمر رساندند. این آزمایشات، نه‌ فقط الگوى احتمالاتى وضعیت پولاریزاسیون دو فوتون گسیل‌شده از یک اتم کلسیم را دقیقاً مطابق با پیش‌بینى‌هاى نظریه کوانتوم نشان مى‌داد، بلکه در آزمایش سوم، از آنجاکه ادوات محاسباتى حداقل ١٣ متر از هم فاصله داشتند (و لذا دو ذره، به معنایی ماکروسکوپیک از یکدیگر «جدا» بودند)، امکان تعیین احتمال «تأثیر بلافصل» محاسبه پولاریزاسیون یک فوتون بر راستاى پولاریزاسیون فوتون دیگر نیز وجود داشت. آزمایش سوم تیم اسپه واضحاً نشان داد که چنانچه معیار «واقعیت» به روایت EPR را بپذیریم، ناگزیریم آنچه در عمل دیده شده را، پیرو اینشتین – اما نه این‌بار با طعنه، بلکه «واقعاً» – «کنش شبح‌وار از راه دور» بنامیم. این در حالی است که با رد التزاممان به روایت تقلیل‌پذیر از علیّت، چنین کنشی دیگر «شبح‌وار» نخواهد بود. امروزه به چنین پدیده‌ای اصطلاح «درهم‌تنیدگی کوانتومی» (Quantum Entanglement) اطلاق می‌شود.

اگرچه آزمایشات EPR به خودى خود به منزله اثبات فیزیکى رابطه مکملیت نیستند، اما واضحاً حکایت از این دارند که معیار «واقعیت» به روایت EPR (یا‌‌ همان روایت «تقلیل‌پذیر» از رابطه علیت، که قرن‌ها قوام منطقى تصویر علمی از جهان را تضمین مى‌کرد)، واقعیت «ندارد»، و نظریه کوانتوم را بایستی توصیفی کامل از طبیعت پنداشت. از همین‌روست که فیزیکدان آمریکایی هنری استاپ، تحلیل بل از معمای EPR را «ژرف‌ترین کشف علم» می‌نامد، چراکه بدین‌وسیله علم، خود را به چالش کشید.

واقعیت، مکملیت، و معمای «زبان»

استنباط «دلیل» اینکه الگوی رنگ‌بندی عکس لباس بلیسدل «چرا» به دو صورت دیده می‌شود منطقاً همان‌قدر امکان‌ناپذیر است که استنباط «دلیل» این‌که چرا نمی‌توان سرعت و مکان دقیق یک ذره زیراتمی را همزمان محاسبه کرد. در واقع چنین «دلیل» بین‌الاذهانی و ابژکتیوی وجود ندارد، چراکه هیچ مؤلفه‌ای از واقعیت نمی‌تواند همزمان به دو معیار مانعه‌الجمع ملتزم باشد.

از همین‌روست که روایت تقلیل‌پذیر از علیت، تصویر کاملی از واقعیت در اختیارمان قرار نمی‌دهد؛ و این را تنها در موارد همپوشانی معیارهای ناظر بر دو واقعیت مانعه‌الجمع می‌توان متوجه شد (همچون خواص موجی و ذر‌ه‌ای نور). نیلز بور با معرفی رابطه «مکملیت» کوشید به رد التزام فیزیکدانان به تصویر تقلیل‌پذیر از علیت بپردازد، و ویتگنشتاین در دوران متأخر فکری‌اش، با ارائه تحلیل بی‌سابقه‌ای از نحوه صورت‌بندی مفاهیم کلاسیک در زبان روزمره، از تقلیل‌ناپذیری متقابل مفاهیم کلاسیک پرده برگرفت. تحولات فیزیک کوانتوم در حدفاصل دهه‌های ۱۹۲۰ تا ۸۰ میلادی نیز آشکارا خبر از تناظر معناداری بین الگوهای شناختمان از جهان پیرامون و نحوه سامان‌بندی مفاهیم کلاسیک در ساحت زبان روزمره می‌داد.

«زبان» هم‌اینک به معمایی ژرف‌تر از صرف و نحو واژه‌ها بدل شده بود، و شرایط آن‌قدر مهیا بود تا فیزیکدان برجسته‌ای همچون بور بنویسد: «ما انسان‌ها به چه اتکا داریم؟ ما به کلمات اتکا داریم… کار ما انتقال تجربیات و ایده‌هایمان به دیگران است. ما بایستی مدام بکوشیم تا چشم‌انداز توصیفمان را وسعت بدهیم، اما به‌ گونه‌ای که پیام‌هایمان صبغه ابژکتیو یا غیرمبهمشان را از دست ندهند…. ما چنان در زبانمان معلق‌ایم که نمی‌توانیم بگوییم کجا بالاست و کجا پایین. واژه «واقعیت» نیز یک واژه است؛ واژه‌ای که ما باید یاد بگیریم که چطور از آن به‌درستی استفاده کنیم».